Euler–Mascheroni constant
| List of numbers – Irrational and suspected irrational numbers γ – ζ(3) – √2 – √3 – √5 – φ – ρ – δS – α – e – π – δ |
|
| Binary | 0.100100111100010001... |
| Decimal | 0.5772156649015328606065... |
| Hexadecimal | 0.93C467E37DB0C7A4D1BE... |
| Continued fraction | [0; 1, 1, 2, 1, 2, 1, 4, 3, 13, 5, 1, 1, 8, 1, 2, 4, 1, 1, … ][1]
(This continued fraction is not periodic. Shown in linear notation) |
The Euler–Mascheroni constant (also called Euler's constant) is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter γ (gamma).
It is defined as the limiting difference between the harmonic series and the natural logarithm:
Its numerical value to 50 decimal places is
 should not to be confused with the base of the natural logarithm, e, which is sometimes called Euler's number.
should not to be confused with the base of the natural logarithm, e, which is sometimes called Euler's number.
Contents |
History
The constant first appeared in a 1735 paper by the Swiss mathematician Leonhard Euler, titled De Progressionibus harmonicis observationes (Eneström Index 43). Euler used the notations C and O for the constant. In 1790, Italian mathematician Lorenzo Mascheroni used the notations A and a for the constant. The notation γ appears nowhere in the writings of either Euler or Mascheroni, and was chosen at a later time because of the constant's connection to the gamma function. For example, the German mathematician Carl Anton Bretschneider used the notation γ in 1835.[2]
Appearances
The Euler–Mascheroni constant appears, among other places, in the following: ('*' means that this entry contains an explicit equation)
- Expressions involving the exponential integral*
- The Laplace transform of the natural logarithm
- The first term of the Taylor series expansion for the Riemann zeta function*, where it is the first of the Stieltjes constants*
- Calculations of the digamma function
- A product formula for the gamma function
- An inequality for Euler's totient function
- The growth rate of the divisor function
- The calculation of the Meissel-Mertens constant
- The third of Mertens' theorems*
- Solution of the second kind to Bessel's equation
- In Dimensional regularization of Feynman diagrams in Quantum Field Theory
- The mean of the Gumbel distribution
- The answer to the Coupon collector's problem*
For more information of this nature, see Gourdon and Sebah (2004).
Properties
The number γ has not been proved algebraic or transcendental. In fact, it is not even known whether γ is irrational. Continued fraction analysis reveals that if γ is rational, its denominator must be greater than 10242080.[3] The ubiquity of γ revealed by the large number of equations below makes the irrationality of γ a major open question in mathematics. Also see Sondow (2003a).
For more equations of the sort shown below, see Gourdon and Sebah (2002).
Relation to gamma function
γ is related to the digamma function Ψ, and hence the derivative of the gamma function Γ, when both functions are evaluated at 1. Thus:
This is equal to the limits:
Further limit results are (Krämer, 2005):
A limit related to the Beta function (expressed in terms of gamma functions) is
Relation to the zeta function
γ can also be expressed as an infinite sum whose terms involve the Riemann zeta function evaluated at positive integers:
Other series related to the zeta function include:
The error term in the last equation is a rapidly decreasing function of n. As a result, the formula is well-suited for efficient computation of the constant to high precision.
Other interesting limits equaling the Euler–Mascheroni constant are the antisymmetric limit (Sondow, 1998)
and
Closely related to this is the rational zeta series expression. By peeling off the first few terms of the series above, one obtains an estimate for the classical series limit:
where ζ(s,k) is the Hurwitz zeta function. The sum in this equation involves the harmonic numbers, Hn. Expanding some of the terms in the Hurwitz zeta function gives:
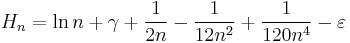 , where
, where 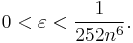
Integrals
γ equals the value of a number of definite integrals:
Definite integrals in which γ appears include:
One can express γ using a special case of Hadjicostas's formula as a double integral (Sondow 2003a, 2005) with equivalent series:
An interesting comparison by J. Sondow (2005) is the double integral and alternating series (A094640)
It shows that 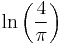 may be thought of as an "alternating Euler constant".
may be thought of as an "alternating Euler constant".
The two constants are also related by the pair of series (see Sondow 2005 #2)
where N1(n) and N0(n) are the number of 1's and 0's, respectively, in the base 2 expansion of n.
We have also Catalan's 1875 integral (see Sondow and Zudilin)
Series expansions
Euler showed that the following infinite series approaches  :
:
The series for  is equivalent to series Nielsen found in 1897:
is equivalent to series Nielsen found in 1897:
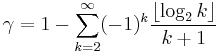 .
.
In 1910, Vacca found the closely related series:
where  is the logarithm to the base 2 and
is the logarithm to the base 2 and  is the floor function.
is the floor function.
In 1926 he found a second series:
From the Kummer-expansion of the gamma function we get:
Series of prime numbers:
Asymptotic expansions
γ equals the following asymptotic formulas (where 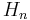 is the nth harmonic number.)
is the nth harmonic number.)
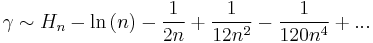
- (Euler)
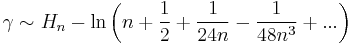
- (Negoi)
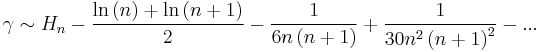
- (Cesaro)
The third formula is also called the Ramanujan expansion.
Relations with the reciprocal logarithm
The reciprocal logarithm function (Krämer, 2005)
has a deep connection with Euler's constant and was studied by James Gregory in connection with numerical integration. The coefficients  are called Gregory coefficients; the first six were given in a letter to John Collins in 1670. From the recursion
are called Gregory coefficients; the first six were given in a letter to John Collins in 1670. From the recursion
we get the table (A002206 and A002207)
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Cn |  |
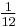 |
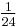 |
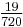 |
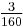 |
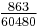 |
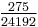 |
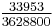 |
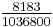 |
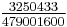 |
Gregory coefficients are similar to Bernoulli numbers and satisfy the asymptotic relation
and the integral representation
Euler's constant has the integral representations
A very important expansion of Gregorio Fontana (1780) is:
which is convergent for all n.
Weighted sums of the Gregory coefficients give different constants:
eγ
The constant eγ is important in number theory. Some authors denote this quantity simply as 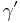 . eγ equals the following limit, where pn is the n-th prime number:
. eγ equals the following limit, where pn is the n-th prime number:
This restates the third of Mertens' theorems. The numerical value of eγ is A073004:
Other infinite products relating to eγ include:
These products result from the Barnes G-function.
We also have
where the nth factor is the (n+1)st root of
This infinite product, first discovered by Ser in 1926, was rediscovered by Sondow (2003) using hypergeometric functions.
Continued fraction
The continued fraction expansion of  is of the form [0; 1, 1, 2, 1, 2, 1, 4, 3, 13, 5, 1, 1, 8, 1, 2, 4, 1, 1, 40, ...] (sequence A002852 in OEIS), and has at least 470,000 terms.[3]
is of the form [0; 1, 1, 2, 1, 2, 1, 4, 3, 13, 5, 1, 1, 8, 1, 2, 4, 1, 1, 40, ...] (sequence A002852 in OEIS), and has at least 470,000 terms.[3]
Generalizations
Euler's generalized constants are given by
for 0 < α < 1, with γ as the special case α = 1.[5] This can be further generalized to
for some arbitrary decreasing function f. For example,
gives rise to the Stieltjes constants, and
gives
where again the limit
appears.
A two-dimensional limit generalization is the Masser–Gramain constant.
Published digits
Euler initially calculated the constant's value to 6 decimal places. In 1781, he calculated it to 16 decimal places. Mascheroni attempted to calculate the constant to 32 decimal places, but made errors in the 20th-22nd decimal places. (starting from the 20th digit, he calculated 1811209008239 when the correct value is 0651209008240.)
| Date | Decimal digits | Author |
|---|---|---|
| 1734 | 5 | Leonhard Euler |
| 1736 | 15 | Leonhard Euler |
| 1790 | 19 | Lorenzo Mascheroni |
| 1809 | 22 | Johann G. von Soldner |
| 1811 | 22 | Carl Friedrich Gauss |
| 1812 | 40 | Friedrich Bernhard Gottfried Nicolai |
| 1857 | 34 | Christian Fredrik Lindman |
| 1861 | 41 | Ludwig Oettinger |
| 1867 | 49 | William Shanks |
| 1871 | 99 | James W.L. Glaisher |
| 1871 | 101 | William Shanks |
| 1878 | 263 | John C. Adams |
| 1952 | 329 | John William Wrench, Jr. |
| 1961 | 1050 | Helmut Fischer and Carl Zeller |
| 1962 | 1,271 | Donald Knuth |
| 1962 | 3,566 | Dura W. Sweeney |
| 1973 | 4,879 | William A. Beyer and Michael S. Waterman |
| 1977 | 20,700 | Richard P. Brent |
| 1980 | 30,100 | Richard P. Brent & Edwin M. McMillan |
| 1993 | 172,000 | Jonathan Borwein |
| 2009 | 29,844,489,545 | Alexander J. Yee & Raymond Chan[6] |
Notes
- ↑ A002852: Continued fraction for Euler's constant On-Line Encyclopedia of Integer Sequences
- ↑ Krämer 2005
- ↑ 3.0 3.1 Havil 2003 p 97.
- ↑ http://mathworld.wolfram.com/MertensConstant.html (15)
- ↑ Havil, 117-118
- ↑ http://www.numberworld.org/nagisa_runs/computations.html
References
- Borwein, Jonathan M., David M. Bradley, Richard E. Crandall (2000). "Computational Strategies for the Riemann Zeta Function". Journal of Computational and Applied Mathematics 121: 11. Derives γ as sums over Riemann zeta functions.
- Gourdon, Xavier, and Sebah, P. (2002) "Collection of formulas for Euler's constant, γ."
- ----- (2004) "The Euler constant: γ."
- Donald Knuth (1997) The Art of Computer Programming, Vol. 1, 3rd ed. Addison-Wesley. ISBN 0-201-89683-4
- Krämer, Stefan (2005) Die Eulersche Konstante γ und verwandte Zahlen. Diplomarbeit, Universität Göttingen.
- Sondow, Jonathan (1998) "An antisymmetric formula for Euler's constant," Mathematics Magazine 71: 219-220.
- ------ (2002) "A hypergeometric approach, via linear forms involving logarithms, to irrationality criteria for Euler's constant." With an Appendix by Sergey Zlobin, Mathematica Slovaca 59: 307-314.
- ------ (2003) "An infinite product for eγ via hypergeometric formulas for Euler's constant, γ."
- ------ (2003a) "Criteria for irrationality of Euler's constant," Proceedings of the American Mathematical Society 131: 3335-3344.
- ------ (2005) "Double integrals for Euler's constant and ln 4/π and an analog of Hadjicostas's formula," American Mathematical Monthly 112: 61-65.
- ------ (2005) "New Vacca-type rational series for Euler's constant and its 'alternating' analog ln 4/π."
- ------ and Wadim Zudilin (2006), "Euler's constant, q-logarithms, and formulas of Ramanujan and Gosper," Ramanujan Journal 12: 225-244.
- G. Vacca (1926), "Nuova serie per la costante di Eulero, C = 0,577…". Rendiconti, Accademia Nazionale dei Lincei, Roma, Classe di Scienze Fisiche, Matematiche e Naturali (6) 3, 19–20.
- James Whitbread Lee Glaisher (1872), "On the history of Euler's constant". Messenger of Mathematics. New Series, vol.1, p.25-30, JFM 03.0130.01
- Carl Anton Bretschneider (1837). "Theoriae logarithmi integralis lineamenta nova". Crelle Journal, vol.17, p.257-285 (submitted 1835)
- Lorenzo Mascheroni (1790). "Adnotationes ad calculum integralem Euleri, in quibus nonnulla problemata ab Eulero proposita resolvuntur". Galeati, Ticini.
- Lorenzo Mascheroni (1792). "Adnotationes ad calculum integralem Euleri. In quibus nonnullae formulae ab Eulero propositae evolvuntur". Galeati, Ticini. Both online at: http://books.google.de/books?id=XkgDAAAAQAAJ
- Havil, Julian (2003). Gamma: Exploring Euler's Constant. Princeton University Press. ISBN 0-691-09983-9.
External links
- Weisstein, Eric W., "Euler-Mascheroni constant" from MathWorld.
- Krämer, Stefan "Euler's Constant γ=0.577... Its Mathematics and History."
- Jonathan Sondow.
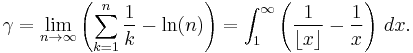
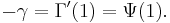
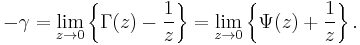
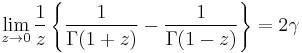
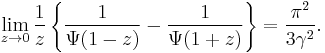
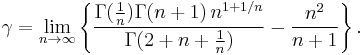
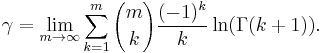
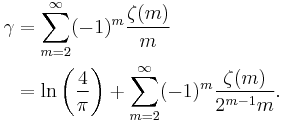
![\begin{align} \gamma &= \frac{3}{2}- \ln 2 - \sum_{m=2}^\infty (-1)^m\,\frac{m-1}{m} [\zeta(m)-1] \\
&= \lim_{n \to \infty} \left [ \frac{2\,n-1}{2\,n} - \ln\,n + \sum_{k=2}^n \left ( \frac{1}{k} - \frac{\zeta(1-k)}{n^k} \right ) \right ] \\
&= \lim_{n \to \infty} \left [ \frac{2^n}{e^{2^n}} \sum_{m=0}^\infty \frac{2^{m \,n}}{(m+1)!} \sum_{t=0}^m \frac{1}{t+1} - n\, \ln 2+ O \left ( \frac{1}{2^n\,e^{2^n}} \right ) \right ].\end{align}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/0767155b9a1613eddb38c057399f5774.png)
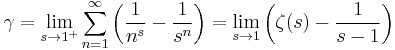
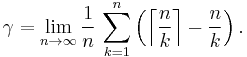
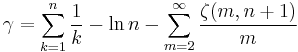
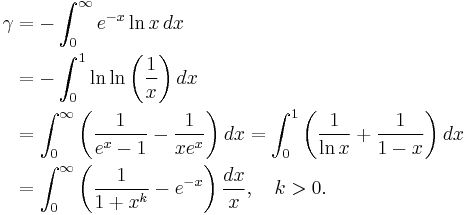
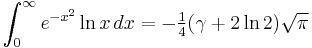
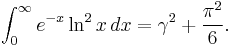
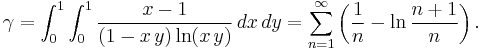
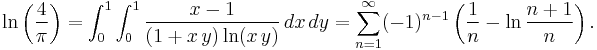
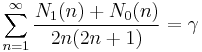
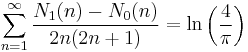

![\gamma = \sum_{k=1}^\infty \left[ \frac{1}{k} - \ln \left( 1 + \frac{1}{k} \right) \right].](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/4d63c2b7a784c70eee25e694674dd103.png)

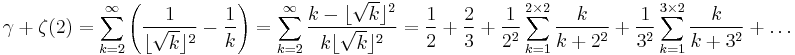
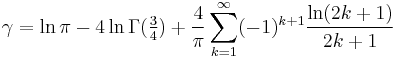



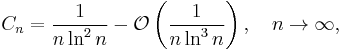


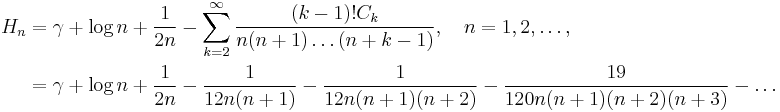
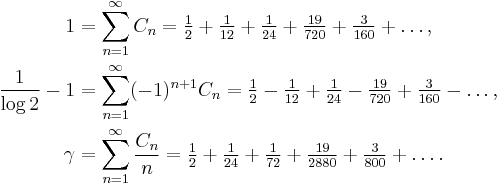
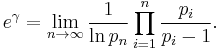

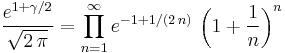

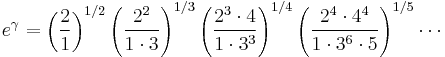
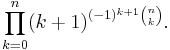
![\gamma_\alpha = \lim_{n \to \infty} \left[ \sum_{k=1}^n \frac{1}{k^\alpha} - \int_1^n \frac{1}{x^\alpha} \, dx \right],](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/3c81568b949b5da901f363aaf7db2ac5.png)
![c_f = \lim_{n \to \infty} \left[ \sum_{k=1}^n f(k) - \int_1^n f(x) \, dx \right]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/2583b7c4faac8342bcf465146003211e.png)
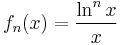
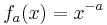
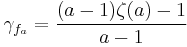
![\gamma = \lim_{a\to1}\left[ \zeta(a) - \frac{1}{a-1}\right]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/992c681ac0050a6135a6b213081f2c06.png)